Magnetic Field Due to an Infinitely Long Current Carrying Straight Wire and Circular Coil

Two very long straight parallel wires, parallel to $y$-axis, carry currents $4I$ and $I$, along $+y$-direction and $-y$-direction, respectively. The wires pass through the $x$-axis at the points $(d, 0, 0)$ and $(-d, 0, 0)$ respectively. The graph of magnetic field $z$-component as one moves along the $x$-axis from $x=-d$ to $x=+d$, is best given by

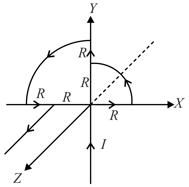
Equal current i is flowing in three infinitely long wires along positive x, y and z directions. The magnitude field at a point (0, 0, -a) would be:

Find the magnetic field at $P$ due to the arrangement shown.

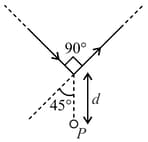
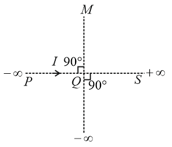
Two mutually perpendicular conductors carrying currents $I_1 \text{and} I_2$ respectively, lie in one plane. Locus of the point at which the magnetic induction is zero, is a:

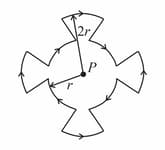
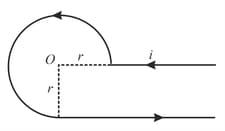
A current I flows around a closed path in the horizontal plane of the circle as shown in the figure. The path consists of eight arcs with alternating radii r and 2r. Each segment of arc subtends equal angle at the common centre P. The magnetic field produced by current path at point P is

Two concentric coils $X$ and $Y$ of radii $16 \mathrm{cm}$ and $10 \mathrm{cm}$ lie in the same vertical plane containing $N-S$ direction. $X$ has $20$ turns and carries $16 \mathrm{A}$. $Y$ has $25$ turns & carries $18 \mathrm{A}$. $X$ has current in anticlockwise direction. The magnitude of net magnetic field at their common centre is-

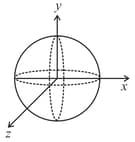
Three rings, each having equal radius R, are placed mutually perpendicular to each other and each having its centre at the origin of co-ordinate system. If current I is flowing through each ring then the magnitude of the magnetic field at the common centre is

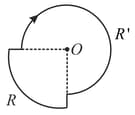
A current of $i$ ampere is flowing through each of the bent wires as shown the magnitude and direction of magnetic field ${\rm O}$ is,

An infinitely long conductor $PQR$ is bent to form a right angle as shown. A current $I$ flows through $PQR$. The magnetic field due to this current at the point $M$ is ${\mathit{\text{H}}}_1$. Now, another infinitely long straight conductor $QS$ is connected at $Q$ so that the current in $PQ$ remaining unchanged. The magnetic field at $M$ is now ${\mathit{\text{H}}}_2$. The ratio $\frac{H_1}{H_2}$ is,

Two coils each of 100 turns are held such that one is in horizontal plane and other in vertical one with their centres coinciding. The radius of the vertical coil is 20 cm and that of the horizontal coil is 30 cm. How would you neutralize the magnetic field of the earth at their common centre? What is the current to be passed through each coil? Horizontal of earth's magnetic induction = 3.49 × 10⁻⁵ T and angle of dip = 30^o. To neutralise the magnetic field at the centre of the coil, the currents is horizontal coil $i_1$ in vertical coil $i_2$  are
 

Find the magnetic induction at point O, if the current carrying wire is in the shape shown in the figure.

Find the magnetic induction at the origin in the figure shown.

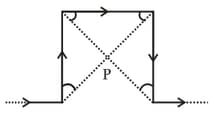
Find the magnetic field at the centre P of square of side a shown in figure.

Two circular coils A and B of radius $\frac{5}{\sqrt{2}}$ cm and 5 cm respectively current 5 Amp. and $\frac{5}{\sqrt{2}}$ Amp. respectively. The plane of B is perpendicular to plane of A their centres coincide. Find the magnetic field at the centre.

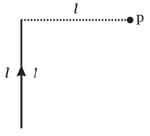
Figure shows a straight wire of length/carrying a current i. Find the magnitude of magnetic field produced by the current at point P.

 

Find out the expression for the magnetic field at a point on the centre of a coil of radius carrying current I and having N number of turns.

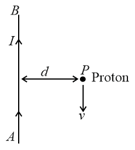
A long straight wire $AB$ carries a current $I$. A proton $P$ travels with a speed $v$, parallel to the wire, at a distance $d$ from it in a direction opposite to the current as shown in the figure. What is the force experienced by the proton and what is its direction?

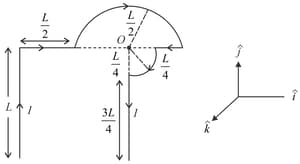
Which one of the following options represents the magnetic field $\overrightarrow{B}$ at $O$ due to the current flowing in the given wire segments lying on the $xy$ plane?

The magnetic field at the centre of a current carrying loop of radius $0.1 \mathrm{m}$ is $5\sqrt{5}$ times that at a point along its axis. The distance of this point from the centre of the loop is(in $\mathrm{cm}$)

The figure shows a metallic cylinder consisting of two metals welded together. The inner core has a radius $R$ while the outer metal occupies the region from $R$ to $2R$ (in meters). The inner core carries a total current of $1 \mathrm{A}$ going into the plane of the figure while the outer region has a uniform current density of $1 \mathrm{A} {\mathrm{m}}^{–2}$ coming out of it.

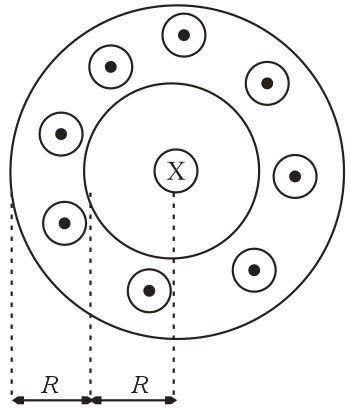
The distance from the centre of the cable at which the magnetic field is zero is